Music interval: the distance between two notes

Have you ever tried to redesign your living room? Let’s say you wanted to get rid of that dusty old couch and get a new one. You would probably measure the available space you have and compare to how big the new couch is, right? Sure, but this only works because we all agree on which measuring system to use. In case you got the couch dimensions in, let’s say, feet, but measured your space in meters, or worse, you got them all in inches but have no idea how long an inch is, then well... good luck! It turns out that intervals in music are exactly the same. The distances between two notes are described by a specific system of measurement and being familiar with that system is key to understanding anything else. Let’s take a quick dive into each one and talk about their expressive nature.

Firstly, let's take a look at how we name notes and the two main systems we use.

The smallest unit: semi-tone

Semi-tone is to an interval what an inch is to a foot. As long as you know how long an inch is, you should know long is a foot. One semi-tone can most easily be seen on a keyboard: it is the smallest distance between two notes in that system (there are smaller intervals in music, but we largely ignore them in the western classical tradition). Take the note C: the distance between C and C# is one semi-tone. Simple right? That’s all there is to it.

Intervals 101

The distance between two notes is described like this: 1) you check how many steps or notes you moved and 2) the number of semi-tones you used.

Let’s use a major 3^rd as an example (don't worry, we'll soon look into thirds in more detail).

The number 3 describes how many notes you moved. So if you start on, let’s say, the note G, a 3^rd above will be 3 notes after

G - A - B

Now that we are in B, the word major tells you if wether we are looking for the B natural or B flat.

As we'll learn, thirds can be minor or major. Minor thirds have 3 semi-tones and Major thirds have 4 semi-tones. So in this case, the major 3^rd brings us to the B natural. If we had a minor 3^rd, we would have arrived at the B flat.

A musical scale contains 7 different notes, so we consider 7 intervals:

2^nd, 3^rd, 4^th, 5^th, 6^th and 7^th

Why do we stop there? Well, the 8^th is the same note we started with but now an octave higher, so the intervals will repeat from this point on. The intervals of a 4^th and a 5^th are special and different from the others and you'll see why. If you don't already know that, just trust me for now, they are. All other intervals have two kinds: minor and major. The 4^th and 5^th can be diminished, perfect or augmented.

 

Dissonance vs Consonance

In short, dissonances are intervals that create tension because they sound harsh to us; while consonances don't create any (or hardly any) tension because they sound “nice”. It’s really as simple as that. Since sounds are just waves in the air around us, we can create an analogy of throwing two little rocks on a pond. If you throw the first rock fast and the second slowly, the ripples will collide and go crazy over each other. That is how your ears perceive a dissonance: the waves of two dissonant notes propagate at very different frequencies. Now imagine if you throw both rocks at the same time with the same intensity. The ripples will interfere with each other but they will soon find a stable and regular balance, which is exactly how your ears perceive a consonance. You'll see this idea of stable/unstable intervals a lot in this post and this is that they mean.

Here is what a consonance sounds like:

And here is what a dissonance sounds like:

If you can't quite hear the difference don't worry, with some practice your ears will start to pick up on these two concepts.

And now, off to the intervals we go!

•••

The unisson

The unison is the most boring interval of all: it happens when two notes are exactly the same, such as C on top of C. For this reason there isn’t much we can do with it. No melody, no harmony. No major, no minor, nothing indeed. A unison interval just is.

The unison is a consonance (the most perfect there is!) and, obviously, a stable interval.

The 2^nd

The first interval we have is called the 2^nd.  Start from any note, the 2^nd will be the first note after that. A to B, E to F, A to G, and do so on. Because seconds are the shortest interval between two notes, they are the most common intervals used in melodies and often referred to as passing notes (or passing tones). If you go from C to E without skipping any notes, you'll pass by D on the way.

An interval of a 2^nd sounds quite harsh, therefore it is not stable and we consider it to be a dissonance.

That means that whenever you hear an interval of a 2^nd played together you should expect it to be “resolved” down. After that interval you expect to hear the C alone, so C and D together would resolve with the D “falling” onto the C.

Minor 2^nd = 1 semi-tone

Major 2^nd = 2 semi-tones

A minor 2^nd will create the strongest tension (therefore strongest attraction to the unison) because it sounds even more dissonant that the major 2^nd.

Here is an example of music that takes great advantage of the tension created by a minor 2^nd (turn up your volume):

Did you pick up on the repeated minor 2^nd intervals up and down right at the beginning?

The 3^rd

Thirds are some of the most common intervals we see in western music! Many country songs are “harmonized” by a second singer. Harmonizing a melody simply means copying it a 3^rd above and singing both lines together. Chords are 2 thirds stacked on top of each other, such as in the C major chord (C – E – G): C to E is a 3^rd and E to G is another 3^rd.

The 3^rd doesn't create any tension, so it is considered a stable and consonant interval.

Minor 3^nd = 3 semi-tones

Major 3^nd = 4 semi-tones

Listen below to how the right hand uses thirds extensively in this famous piano piece. The melody you hear is actually being played with two notes together, a 3^rd apart.

This is a great example of thirds being used to create a sweet and tender sound.

The 4^th and 5^th

Remember from the beginning of this post how the 4^th and 5^th are special intervals? Well, here we go. Both the 4^th and 5^th chords in a given key, together with the first one, form the foundation for music harmony. In short, all chords in a key “gravitate” around their tonal center (the first chord, known as the tonic). That attraction depends on the immutable presence of the 4^th and the 5^th. Change one of them, and the music will stop making any sense because it will lose its main structure.

Needless to say that both perfect 4^th and perfect 5^th are stable and consonant intervals. They are points of resolution and central to our notion of tonality. They may be, however, altered for the sake of dissonance. In that case, those changes will create dissonances that must be immediately resolved. Why do they have to be resolved? There are no keys where the 4^th or 5^th chords are not perfect. If, for example, the 5^th chord in a key is repeatedly played in its augmented form, this music will soon stop making sense and its relationship with the tonic chord will be diluted. If we lower or raise those intervals one step down or one up, we create the following intervals:

Diminished 4^th = 4 semi-tones (dissonant)

Perfect 4^th = 5 semi-tones

Augmented 4^th = 6 semi-tones (dissonant)

Diminished 5^th = 6 semi-tones (dissonant)

Perfect 5^th = 7 semi-tones

Augmented 5^th = 8 semi-tones (dissonant)

Let's see an example of a perfect 5^th in the movies!

The opening notes in this theme are perfect fifths. In fact this interval is part of the theme in this music and we hear it all over the place.

•••

The Devil's Interval

Let's take a quick break to talk a little bit about a very important and, at one time, controversial interval. The augmented 4^th is the most dissonant interval of all. It is so harsh and bizarre that it has its own nickname: the tritone. A tritone creates an incredible tension when played together, listen to how Camille Saint-Saëns used the tritone to create a bizarre, evil like theme in this piece

Hear that harsh sound from the violin at second 18? That is what the tritone sounds like. During the middle ages this interval was prohibited by the Catholic Church. Composers and theorists at the time considered music to be a direct representation of the image and world of God and thus, the tritone with its harsh and ugly sound was something from the Devil. That is also where the nickname comes from.

Today the tritone is fundamental to our notion of a tonal center in any key precisely due to its incredible tension and instability. The tritone always "resolves" (aka the movement to a consonant interval) into the tonic of the key. It can resolve outwards, where the top note moves one step up and the lower note moves a step down. Or it can resolve inwards, where the top note moves down one step and the lower note moves up a step.

Play a tritone, then move both notes outwards, like on the image below.

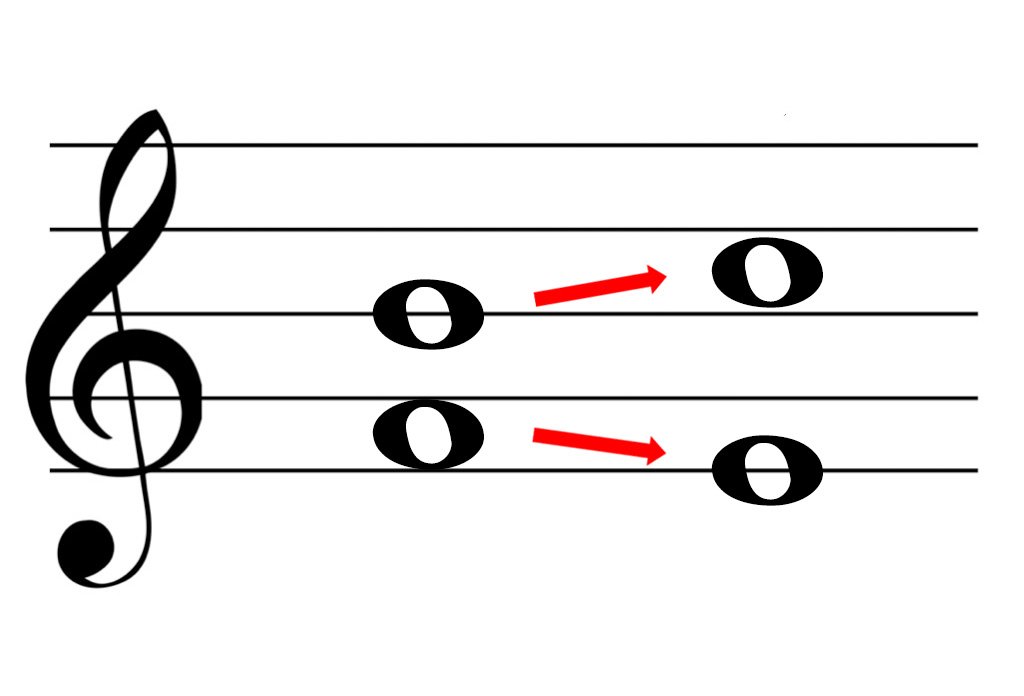
The next interval will be part of the tonic chord of the key. In this example the tritone B and F resolve into C and E, which form the C major chord (C - E - G). Your ears will immediately recognize this sequence as establishing the key of C major.

•••

The 6^th

Much like the 3^rd, the 6^th is a consonant interval. Bring a 6^th one octave below and you’ll have a 3^rd: C to A is an interval of a 6^th, while A to C is an interval of a 3^rd. For that reason much of the characteristics of the 3^rd are shared by the 6^th.

It is a stable and consonant interval, often used to resolve the dissonance created by the tritone.

Minor 6^th = 8 semi-tones

Major 6^th = 9 semi-tones

Listen below to an example of a 6^th being used as an opening to a theme. The first two notes are a major 6^th apart.

This use case is very common and open makes for an expressive and emotional sound.

The 7^th

The interval of a 7^th, much like all other intervals (except for the 4^th and 5^th), can be major or minor. The major 7^th has one special name: we call it the leading tone. The reason for that is because the major 7^th, sits just one semi-tone before the 8^th, which is the tonic (the first note note repeated an octave up). Being so close to the tonic, it creates the greatest attraction to the it and our ears almost beg to hear that tonic after a major 7^th. When we hear the 7^th of a scale together with the 4^th it creates the tritone. The tension created by that interval combined with the presence of the leading tone makes our ears anticipate the resolution even before we hear it.

The 7^th is unstable and dissonant, and it is often used together with the 4^th to create the tritone.

Minor 7^th = 10 semi-tones

Major 7^th = 11 semi-tones

Beethoven knew this very well and played with this idea in his first symphony. Listen to the first 23 seconds in the example below:

Before the music even begins, Beethoven tricks the audience by establishing three different tonalities. In this example we hear three different tritones followed by their resolutions. Each of these new chords can be the key of the piece and it is only on the third one that we understand where the music is actually going. Beethoven seems to be searching for the "right key" until the third tritone. Then he repeats that one 3 times (probably not a coincidence we see so many 3 everywhere, but that is a topic for a different discussion) as if he was saying: here it is, I found the key I was looking for!

Final thoughts

As we explored in this short post, intervals form the basis for the understanding of music. Not only do they tell you the exact distance between two notes, but also carry a specific expressive character and behavior. Music is a complex art, with many moving parts and each one made up of various layers. They are all interconnected and delicately balanced by a few fixed rules and conventions. Understanding how intervals work will give you a solid ground to walk on as you continue learning more about the inner workings of this fascinating art form.